It's almost like a coinflip is a 50% gamble.
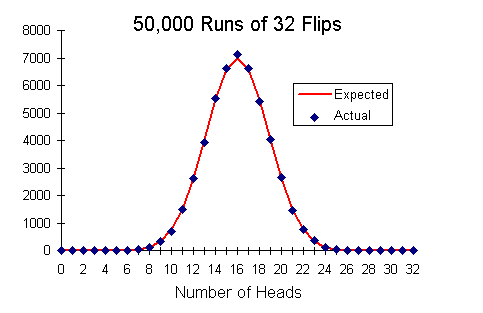
When something is binomially distributed like this (IE it either happens or it doesn't,) the odds of any one outcome can be calculated. In the case of a 50% chance (X~B(0.5,Y), where Y is the sample size,) the graph resembles a normal distribution (that is, this graph here:)
The expected graph is symmetrical, and out of any sample, the modal value is exactly half.
Basically, the more you gamble the more and more your results will tend towards the mean value of 1/2, also known as a break even.
I mean, you have a relatively high chance of being just over break even, but that same chance is replicated in the negatives.
So what's the point in gambling? Idfk funny I guess.